Chess960, freestyle chess, or Fischer Random Chess is a variant of chess that randomizes the starting position by scrambling the major pieces on the back ranks in 960 legal permutations. This variant was introduced in 1996 by former world champion Bobby Fischer—his way of reducing the reliance on opening preparation, forcing players to truly prove their chess understanding and creativity over the board.
The typical setup on a traditional chess board is as follows:

- From the outside in symmetrically, we place a rook, knight, bishop
- On the white side, the king is on the right side of the middle and the queen is on the left
- On the black side, the king is on the left side of the middle and the queen is on the right
- This is so the kings face each other on the opposite side of the board
- The white king is on a black square (for standardization, it makes no difference to the game)
In chess960, the back rank with all the major pieces (the not pawns) is scrambled. The rooks, bishops, knights, queen, and king are moved around from their standard positions. The white and black side are mirrored, just like in normal chess (kings face king, knights face knighs, etc.).

Fischer didn’t simply want to create a new game; he wanted to retain the similar qualities of traditional chess, just with a lesser reliance on opening prep. Therefore, there are two rules to the scrambling:
- You must still be able castle, so the king must be in between the two rooks.
- The bishops must be on different color complexes.
Let me elaborate on them a bit more for clarity:
New Rules of Castling
Castling king-side and queen-side bring the king and it’s castled rook to the same position as in traditional chess. This means there must be no pieces in bewteen the king and the rook before castling, and that there are no other pieces occupying the castling squares before castling. You still cannot castle on check and cannot castle if an opposing piece attacks a square through which the king castles.
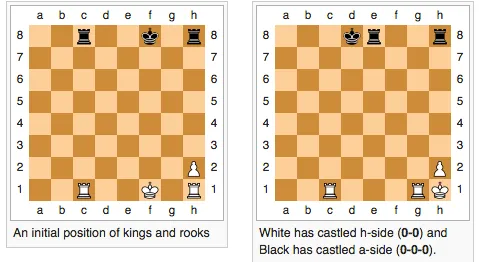
This brings a new dynamic: castling can be much easier (i.e. you can castle on move 1) or much more difficult (you must clear out a bunch of squares before castling). The overall goal to castle can be more or less desirable depending on how much less or more time it takes to castle.
Opposite Colored Bishops
Bishops move diagonally, which means two bishops on opposite color complexes cannot attack one another. As a result, we want to maintain the strategies around opposite-colored bishops. As such, in chess960, we still have one light- and dark-squared bishop.
Opening Preparation
I mentioned Fischer wanted to reduce the reliance on opening prep. Opening prep is essentially when players record potential positions from the beginning of the game, looking at the best moves for both white and black, hoping to find positions where they can have an edge over their opponent—either in familiarity, knowledge, sharpness, or positional advantage.
Before the age of computer chess engines, players would work in teams (or individually, if you’re the GOAT like Fischer) to map out potential opening lines (i.e. move sequences) that give you a leg up on your opponent. If you learn a particular line well, you won’t have to think nearly as much as your opponent and can get them in uncomfortable territory very quickly. On the other hand, you might prepare refutations to your opponent, trying to find the same lines as your opponent so you will be ready when they come for you.
Back then, you had to be quite creative to find opening advantages—you would have to spend a lot of time preparing for particular opponents, hoping to find any line that will secure you an advantage. It often required teams days, weeks, or months to squeak out an edge.
After an opening is tested in a game, it becomes public domain. Others begin to analyze this new weapon and they can prepare refutations against it. As such, the line becomes dead once enough players become familiar with it. At the top level, most openings are discarded in favor of ones that are more flexible, well known, or have some sort of stability. Players rarely go for super risky lines, since they can be destroyed very quickly if one’s opponent is strong enough.
Even back then, Fischer began to notice the reliance on opening prep. The sport of chess began to be a battle of preparation, where players had to spend endless time studying up openings in order to be competitive. A lot of the game was played before any game actually began, played out in prep camps. Countries or teams with many strong grandmasters (like Russia) had an edge over their less-prepared opposition. Fischer was dissatisfied. To address the reliance on rote memorization, he invented chess960 to bring strategic thinking back to the game.
Nowadays, people have access to fast computer engines that simply transcend the capability any human will ever have. Instead of spending days finding a potential new opening, you can pretty much know the best opening lines right off the bat. All modern players prepare lines that are 20+ moves long with engines and can analyze any new opening in just a few minutes. As a result, openings are simply dying. Any new idea gets squashed in a matter of weeks. It’s beginning to become impossible to squeak out an opening advantage, since everyone knows all the top lines already.
Grandmasters are opting for subpar opening choices instead, hoping that their opponent simply cannot find the best continuations from any position, even though their position is objectively not the best. This is a tricky dilemma, because you place yourself in a less favorable position in the hopes that your opponent does not find the best line—it’s a gamble.
Time Controls
All chess games are played on a time control, which means each player has a certain amount of time at the start to play. If the time expires, the player forfeits the game.
There are more complicated rules about running out of time relating to the final position, but I won’t cover that here.
The time controls are typically in the form T+t, where
- T is the amount of time you start with
- t, also called increment, is the amount of time you get back every time you make a move
For example 5min+1sec means you start with 5 minutes and you get 1 second back every time you make a move. We generally denote this 5+1 for short. Many online games have 0 second increment, which means you get no time back when you make a move.
Games are broadly classified by the amount of time you begin with:
- Bullet: 0-2min, typically with 0 or 1 second increment
- Blitz: 3-5min, typically with 0-2 second increment
- Rapid: 10-20min, with 0-15 second increment
- Classical: 30+min, airing on the magnitude of hours (1, 2 hours).
- Classical has more complicated rules. Usually, the game is split into segments, where you can get an extra 30 minutes on move 40, or maybe you get a 10 or 30 second increment starting move 60.
When players know an opening well, they can blitz out many moves in a row at the beginning without having to think. This is advantageous in all time controls. It’s common to see players blitz out 10 or 15 moves without taking any time to think at all. This is because the game always starts in the same position, and professionals are familiar with most of the top lines.
In classical games, players tend to have a good amount of time to think. Good players tend to play strong moves, and the games are more likely to end in a draw. Back before engines, players relied on their prep to squeak out the initial advantage, but in the age of engines, players can play the refutation lines to bring the game closer to a draw. Everyone knows the same lines, and it requires a lot of effort to find something new, or to prepare a subpar line that may cause your opponent to screw up. It’s simply not as interesting as it used to be.
Quick aside: It’s known that the player with the white pieces has an ever-so-slight advantage, as they dictate the first move. It’s not much, but it is something. The black player looks for equality (looking to reduce that slight advantage to zero), while the white player fights to maintain the advantage. To lose the advantage means the white player must have made mistakes.
In faster time controls, opening prep is more and less important at the same time. Players have less time to think and tend to make subpar moves. This makes it both harder to capitalize on an opening advantage or makes it more difficult to refute a novel opening. Players can make mistakes in the opening, middle game, or endgame, and games are decided by all sorts of mistakes that player wouldn’t make if they had more time. As a result, players can always choose to alternate their openings to find something they’re more familiar with, and the games will get interesting simply because players tend to make more mistakes with less time. It becomes more-so a battle of speed, quick calculation, intuition, and time management.
Once the game reaches a more traditional position (say, after castling or once pieces have been traded off), chess960 reverts back to a battle of traditional chess ideas. But once you get to this point, the game revolves much more around understanding, not brute memorization. It’s how Bobby Fischer intended this game to be.
Benefits of Chess960
In chess960, you don’t really know what the starting position is going to be until a few moments or an hour before the game begins. Preparation becomes almost impossible with 960 possible opening positions. As a result, players can’t simply blitz out 10-20 moves at the beginning of the game. Each move requires careful planning and understanding of the game.
Some traditional chess ideas are universal that translate into chess960 well, and some do not. As a player, you have to know which ones work well when and which ones don’t. This forces players to be more careful, more deliberate, and more proactive. Even in games at a professional level, you might see grandmasters make mistakes within the first few moves.
For most normal players, chess960 is just a fun variant. Most of us plebs have little capacity or time to understand the game of chess in a way that these professionals do. We can memorize openings but we probably barely understand them. We don’t play for money, and nobody pays to watch us play. For most normal people, the game does not revolve around the opening as it does for the top professionals. Luckily, we can all continue to play traditional chess like cavemen; but for the elite of the elite, they’re looking for more of a challenge.
Former world chess champion and rank no. 1 player Magnus Carlsen has expressed his dissatisfaction over the last few years on opening prep, claiming the game simply is not as fun or exciting as it used to be. He and a lot of the other top grandmasters have begun advocating for playing professional chess960 tournaments instead, hoping to bring back some creativity and ingenuity back into the sport.
As of a few years ago, many professional tournaments have featured chess960 instead. The games seem to be more exciting and riddled with mistakes, and these professionals are forced to think from move 1. Although chess960 is becoming more popular, most spectators are still looking to watch normal chess, a game most of us have not conquered yet.
Why are there 960 positions?
Oh yeah, I wrote this post to explore how we actually arrive at the 960 chess960 positions. Let’s get back to that.
I wanted to bring two intuitive ways of calculating the 960 Fischer Random positions using two counting techniques. This is not an introduction, so I advise you to learn some basic combinatorics before reading this if you aren’t familiar.
The only thing you really need is to understand the concept of n choose k, which, as its name suggests, counts the number of ways you can pick k distinct objects with a total of n distinct objects. This has mathematical notation: $$n \choose k$$ For example, you have 5 friends and a car that can fit 3 people to go to Starbucks. To pick 3 people out of the 5 to go get coffee, there are 5 choose 3 = 10 ways of doing so. To learn its formula and derivation, read more here. As long as you assume this formula holds, you can read it and just assume the numbers work out :).
As mentioned earlier, there are only two rules:
- King between rooks
- One bishop is on a light square, one bishop is on a dark square.
It’s not trivial to see how we tackle this. If we place any piece first, that interferes with our rules. If we place a piece on a light square, that leaves one less square for the light-squared bishop. If we place a knight on the left edge, then we know a king can’t go on its immediate right, as it would not be in between the rooks. Therefore…
Method 1: Casework
My first approach was to consider placing the king and rooks first. This is the most restrictive method, since we know we must place one rook, one king on the right, and another rook on the king’s right. If we place the rook and kings in some RKR (king between rooks) arrangement, we can fill up the space around it however we please, as long as we put one bishop per colored square.
So how many ways are there to place the rooks and king? Complementary counting doesn’t seem to be super useful since we have to find all the positions where the king is on the left and which ones are on the right.
So, let’s just pick three squares for the RKR to go. There are 8 squares per rank, and we choose 3 of them, which is simply:
$$8 \choose 3$$
This is all the ways we can choose the three slots for the two rooks and the king. Within these three slots, we can place them arbitrarily with 3! possibilities. But only one is valid, which is the position RKR. Therefore, 8 choose 3 simply is the number of ways we can place the RKR.
However, this becomes slightly tricky when we want to place the bishops, since the combinations depends on how many of each square complex are remaining. For example, all three RKR could be on white or all three black. Two could be on white, one on black or vice versa. Therefore, we must use casework.
Case 1: RKR all on white or black
Without loss of generalization, let’s say RKR are all on the white squares. On each rank of 8 squares, half are white, half are black, alternating, so we have 4 of each color.
The number of ways to pick RKR all on white means we pick 3 white squares from 4, or:
$$4 \choose 3$$
We have 1 remaining white square and 4 of our original black ones. We know one of the bishops must be white, so there is only 1 possible choice. Out of the remaining 4 pieces, we pick 2 squares for the knights (they are indistinguishable) and one square for the bishop, leaving the one remaining square for the queen. This is:
$${4 \choose 2}{2 \choose 1}$$
That’s it! We multiply by two, since the combinations are exactly the same if RKR are all on black squares as well. In total, we have:
$$2 \cdot {4 \choose 3}\cdot{4 \choose 2} \cdot{2 \choose 1}=\boxed{96\ \text{combinations}}$$
Case 2: Two are on one color and one on the other
We can split up RKR to two of one color, one of the other. This exhausts our cases, as there are only two color complexes. WLOG, let’s say two pieces are white and one piece is black.
For RKR placement, we choose two white squares and one black squares. With 4 of each, this is:
$${4 \choose 2}\cdot{4 \choose 1}$$
For the bishop placements, we know one bishop must be white and one is black. There are 2 remaining white squares and 3 remaining black squares, so we count:
$${2 \choose 1} \cdot {3 \choose 1}$$
Now, we place the knights and the queen. It doesn’t matter which complex any of them go on. We have 3 remaining squares and we choose 2 for the knights, leaving one for the queen:
$$3 \choose 2$$
We can multiply by 2 for the symmetric case where two pieces are on black and one piece is on white. In total, we have:
$$2 \cdot {4 \choose 2}\cdot{2\choose 1} \cdot {2\choose 1}\cdot{3 \choose 1} \cdot {3 \choose 2} = \boxed{864 \ \text{combinations}}$$
Putting it together
Putting these two cases together, we have:
$$864+96=\boxed{960\ \text{combinations}}.$$
We did it!
Method 2: Being smart
One thing you might notice is that we don’t need to place the rooks and king first. It might be a more restrictive rule, but it doesn’t need to be considered first. If we consider the bishops first, we realize the rule doesn’t interfere with the RKR combinations, which wasn’t true the other way around. If we place one white and black bishop, we can place the RKR independently that still covers all combos.
Placing Bishops
There are 4 white and black squares and we pick one square white and black square for each bishop. Simply, this is:
$${4 \choose 1} \cdot {4 \choose 1}$$
Placing RKR
We realize that these bishops can be wherever. With the remaining 6 locations, we can just pick the squares for RKR which represents all RKR spaces with the combos for the bishops; the bishop restrictions is pretty much independent to king placement. Similar to the logic in method 1, we have 6 spaces and 3 choices:
$$6 \choose 3$$
There is only one valid RKR placement per combo, so we are done.
Rest of the pieces
We now place the queen and the knights. With three arbitrary squares remaining, there are 2 choices for the knights and one remaining for the queen:
$${3 \choose 2} \cdot {2 \choose 1}$$
Putting it together
These are all independent, so we can multiply them together to get:
$${4 \choose 1}\cdot{4 \choose 1}\cdot{6 \choose 3}\cdot{3 \choose 2} = \boxed{960\ \text{combinations}}.$$
Much easier!
Combo Conclusion
I thought of method 1 first since it was more intuitive, but the second way is probably just as intuitive and much faster. Was a fun exercise.
Actual Conclusion
I always hear chess960 this chess960 that, but I never knew exactly why there were 960 positions, so I took that as an exercise for myself today. It feels good to know how things around me work, and it’s a continuing challenge to understand everything else around me, like microwaves, traffic lights, elevators, and more.
I also got to use this as an excuse to talk about chess again, which is good for me. You can thank the Freestyle Chess Grand Slam tournament happening in Vegas at this moment. Hope you learned something!
